Hash算法的用途
- 产生全局唯一标识 尽管不可能,不过小范围内可行,下面会讨论。
- 校验和(Checksum) 其实Checksum和Hash还是有区别的,看这里。
- 密码安全 一般主要用来做密码的签名,例如在数据库里存放MD5后的密码。如果要保证密码的安全,防止被彩虹表攻击,可以加盐(Salt)。
- Hash表索引 这个应该最常用的。
Hash算法随用途的不同而不同,例如校验和(Checksum)Hash算法需要尽量高效、快速(如CRC),而在密码安全是则必须低效、缓慢从而避免被暴力破解(如MD5、SHA-1等)。
理想中的Hash算法的一个共同特点那就是产生的值是随机和唯一的,但根据鸽子窝原理(pigeonhole principle)这是不可能的,但是碰撞发生的概率大体是怎么分别的呢?
生日悖论
这个Hash的碰撞问题其实与生日悖论(Birthday problem)一样:
如果一个班级上有30个同学,则至少出现两个人同生日的概率是多少?(假设不考虑闰年,一年365天)
归纳一下问题变成:
假设从集合m中取n个(n > 0, n <= m),则取出相同的概率是多少?
用高中的组合数学得到公式如下:

因为k/m远远小于1(k为30,m为365),可以用泰勒级数的一级近似表示


最后得到结果:
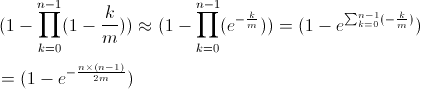
这样可以算出生日悖论里的概率来:
30个人中有同生日的概率P(30) = 70%
70个人中有同生日的概率P(70) = 99% (这个足够让人惊讶了,这就是为什么叫悖论的原因了:))
概率的分布图:

Hash算法的碰撞概率
假设Hash算法是随机的,根据以前的公式得到碰撞的概率P(m,n),m代表Hash产生的个数(一般为2^n,MD5为128位,所以为2^128),n为连续Hash的次数,当n值远小于M时用泰勒级数一级近似得到简化的公式:
P(m,n) = 
Hash多少次以后碰撞的概率为50%呢?也就是根据概率和m求出n:
N(p, m) = 
16位Hash碰撞概率为50%,则n = 301次
32位Hash碰撞概率为50%,则n = 77162次
128位MD5碰撞概率为50%,则n = 21,719,381,355,163,562,492次
参考
http://en.wikipedia.org/wiki/Birthday_paradox
http://www.codinghorror.com/blog/2007/12/hashtables-pigeonholes-and-birthdays.html
